[Перевод] Математика игры 204807.10.2017 13:18

Часть 1. Расчёт минимального количества ходов для победы с помощью цепей Маркова

После недавнего обновления экран «You win!» игры 2048 начал показывать количество ходов, потребовавшихся для победы, и я задался вопросом: сколько же нужно ходов, чтобы выиграть?

В первой части статьи мы ответим на этот вопрос, смоделировав игру 2048 в виде цепи Маркова и проанализировав её, чтобы показать, что вне зависимости от мастерства игрока для победы в среднем нужно не менее 938,8 ходов. Это даёт нам неплохое мерило отсчёта — если вы можете выигрывать примерно за такое количество ходов, то неплохо играете.

Количество ходов, необходимых для победы, зависит от случайности, потому что игра добавляет тайлы 2 и 4 случайным образом. Анализ также покажет, что распределение минимального количества ходов до победы имеет стандартное отклонение в 8,3 хода, и что его общая форма хорошо аппроксимируется смесью биномиальных распределений.

Чтобы получить эти результаты, мы воспользуемся упрощённой версией 2048: вместо размещения тайлов на поле, мы… будем бросать их в мешок. То есть мы проигнорируем геометрические ограничения, вводимые формой поля, на которой могут объединяться тайлы. Такое упрощение сильно облегчит нашу работу, потому что игроку больше не придётся принимать никаких решений 1, и потому что нам не нужно будет отслеживать положение тайлов на поле.

Ценой избавления от этих геометрических ограничений будет то, что мы сможем вычислить только нижнюю границу ожидаемых ходов до победы; может случиться так, что геометрические ограничения не позволят достичь этой границы. Однако, сыграв множество партий в 2048 (ради науки!), я также покажу вам, что на практике мы часто можем приблизиться к этой границе.

Если вы незнакомы с 2048 или с цепями Маркова, то не волнуйтесь — я буду объяснять необходимые понятия по ходу статьи. Код (исследовательского качества), на основе которого написана статья, имеет открытые исходники, на случай, если вы захотите изучить код для генерирования цепи и графиков.

2048 как цепь Маркова

Чтобы представить нашу упрощённую игру »2048 в мешке» как цепь Маркова, нам нужно задать состояния и переходные вероятности цепи. Каждое состояние — это что-то вроде «слепка» игры в определённый момент времени, а переходные вероятности задают для каждого состояния вероятность перехода в него.

Здесь мы закодируем каждым состоянием тайлы, находящиеся в данный момент в мешке. Нас не волнует порядок тайлов, поэтому мы можем воспринимать их как множество тайлов. Изначально в мешке нет тайлов, то есть начальное состояние — это просто пустое множество. В виде схемы, которую мы добавим ниже, это начальное состояние выглядит как:

Подготовка поля

Montage of a sample of eight setup states.

Пример дюжины полей для новой игры.

Когда мы начинаем новую игру в 2048, игра располагает на поле два случайных тайла (см. примеры выше). Чтобы представить это в цепи Маркова, нам нужно задать переходные вероятности из начального состояния в каждое из возможных последующих состояний.

К счастью, мы можем посмотреть на исходный код игры, чтобы понять, как игра это делает. Когда игра размещает на поле случайный тайл, она всегда следует такому сценарию: выбирает случайным образом клетку, затем добавляет новый тайл, либо со значением 2 (с вероятностью 0,9), либо со значением 4 (с вероятностью 0,1).

В случае »2048 в мешке» нас не волнует поиск свободной клетки, потому что мы не ставили никаких ограничений на ёмкость мешка. Нас интересует только добавление тайла 2 или 4 с заданной вероятностью. Это приводит к трём вероятным последующим состояниям из начального состояния:

$\left \{ 2,2 \right \}$ , когда оба новых тайла имеют значение 2. Это происходит с вероятностью $0,9 \times 0,9 = 0,81$ .
$\left \{ 4,4 \right \}$ , когда оба новых тайла имеют значение 4. Это происходит с вероятностью $0,1 \times 0,1 = 0,01$ , то есть вам довольно сильно повезло, если вы начинаете игру с двумя четвёрками.
$\left \{ 2,4 \right \}$ , когда новые тайлы имеют значение 2, а потом 4, что происходит с вероятностью $0,9 \times 0,1 = 0,09$ , или сначала 4, а потом 2, что происходит с вероятностью $0,1 \times 0,9 = 0,09$ . Нас не волнует порядок, поэтому оба случая приводят к одному состоянию с общей вероятностью .

Мы можем добавить эти последующие состояния и их переходные вероятности в схему цепи Маркова следующим образом (переходные вероятности записаны на рёбрах, а новые узлы и рёбра обозначены синим):

Directed graph showing the initial state and its immediate successors: {2, 2}, {2, 4}, {4, 4}

Играем в игру

Разместив первую пару тайлов, мы готовы начать игру. В реальной игре это бы значило, что игроку нужно провести влево, вправо, вверх или вниз, чтобы соединить пары одинаковых тайлов. Однако в нашей игре с мешком ничего не мешает нам соединить все пары одинаковых тайлов, поэтому так мы и сделаем.

Правило объединения тайлов в игре с мешком будет следующим: находим в мешке все пары тайлов, имеющие одинаковое значение, и удаляем их; затем заменяем каждую пару тайлов одним тайлом с удвоенным значением 2.

После объединения пар одинаковых тайлов для перехода к последующему состоянию игра случайным образом добавляет один новый тайл, воспользовавшись уже описанным выше процессом, то есть тайл 2 с вероятностью 0,9 или тайл 4 с вероятностью 0,1.

Например, чтобы найти возможные последующие состояния состояния $\left \{ 2,2 \right \}$ , мы сначала объединяем два тайла 2 в один тайл 4, а затем игра добавляет или тайл 2, или тайл 4. Таким образом, возможными последующими состояниями будут $\left \{ 2,4 \right \}$ и $\left \{ 4,4 \right \}$ , которые, так уж получилось, мы встречали ранее. Тогда схема, содержащая эти два перехода от $\left \{ 2,2 \right \}$ , которые имеют вероятность 0,9 и 0,1, соответственно, будет иметь вид:

Directed graph showing the additional transitions from the {2, 2} state

Если мы продолжим выполнять этот процесс для последующих состояний состояния $\left \{ 2,4 \right \}$ , то увидим, что пока объединение невозможно, потому что нет пар одинаковых тайлов, и последующее состояние будет или $\left \{ 2,2,4 \right \}$ или $\left \{ 2,4,4 \right \}$ , в зависимости от того, будет ли новый тайл иметь значение 2 или 4. Тогда обновлённая схема будет такой:

Directed graph showing the additional transitions from the {2, 4} state

Слои и «пропуски»

Мы можем продолжить добавлять переходы таким образом. Однако при добавлении новых состояний и переходов схемы могут становиться всё более сложными 3. Мы можем немного упорядочить схемы, воспользовавшись следующим наблюдением: сумма тайлов в мешке увеличивается с каждым переходом или на 2, или на 4. Так получается потому, что объединение пар одинаковых тайлов не меняет сумму значений тайлов в мешке (или на поле — это свойство применимо и к реальной игре), а значит, игра добавляет тайл 2 или тайл 4.

Если мы сгруппируем состояния по их сумме в «слои», то первые несколько слоёв будут выглядеть примерно так:

Directed graph showing states up to sum 12

Чтобы снизить зашумлённость схем, для более поздних слоёв я также не указываю пометки для переходов с вероятностью 0,9 (сплошные линии, если они никак не помечены) и 0,1 (пунктирные линии).

При группировке состояний в слои по суммам становится очевидной ещё одна закономерность: каждый переход (кроме перехода из начального состояния) совершается или в следующий слой с вероятностью 0,9, или в слой после него с вероятностью 0,1. (Это особенно очевидно, если посмотреть на слои с суммами 8, 10 и 12 со схемы выше.) То есть чаще всего игра даёт нам 2, и мы переходим на следующий слой, но иногда нам везёт, и игра даёт нам 4, и это означает, что мы можем пропустить слой, что немного приближает нас к цели — достижению тайла 2048.

Конец игры

Мы можем продолжать этот процесс вечно, но поскольку нас интересует только достижение тайла 2048, мы остановим его в этот момент, сделав любое состояние с тайлом 2048поглощающим. Поглощающее состояние имеет единственный переход, который ведёт к нему самому с вероятностью 1. То есть, достигнув поглощающего состояния, выйти из него уже не удастся.

В этом случае все поглощающие состояния являются «состояниями победы» — мы получили тайл 2048, а значит, выиграли игру. В «игре с мешком» нет возможности «проиграть», потому что в отличие от реальной игры, мы не можем попасть в ситуацию, когда поле (или мешок) заполнится.

Первое состояние, содержащее тайл 2048 находится в слое с суммой 2066. Примечательно, что невозможно получить на поле единственный тайл 2048 — для объединения тайлов 1024, тайлов 512, и так далее, требуется несколько ходов, за которые накапливается больше тайлов 2 и 4. Поэтому сумма тайлов для первого состояния с тайлом 2048 выше, чем 2048.

Вот как выглядит граф возле этого первого выигрышного состояния (посмотреть подробнее). Поглощающие состояния выделены красным:

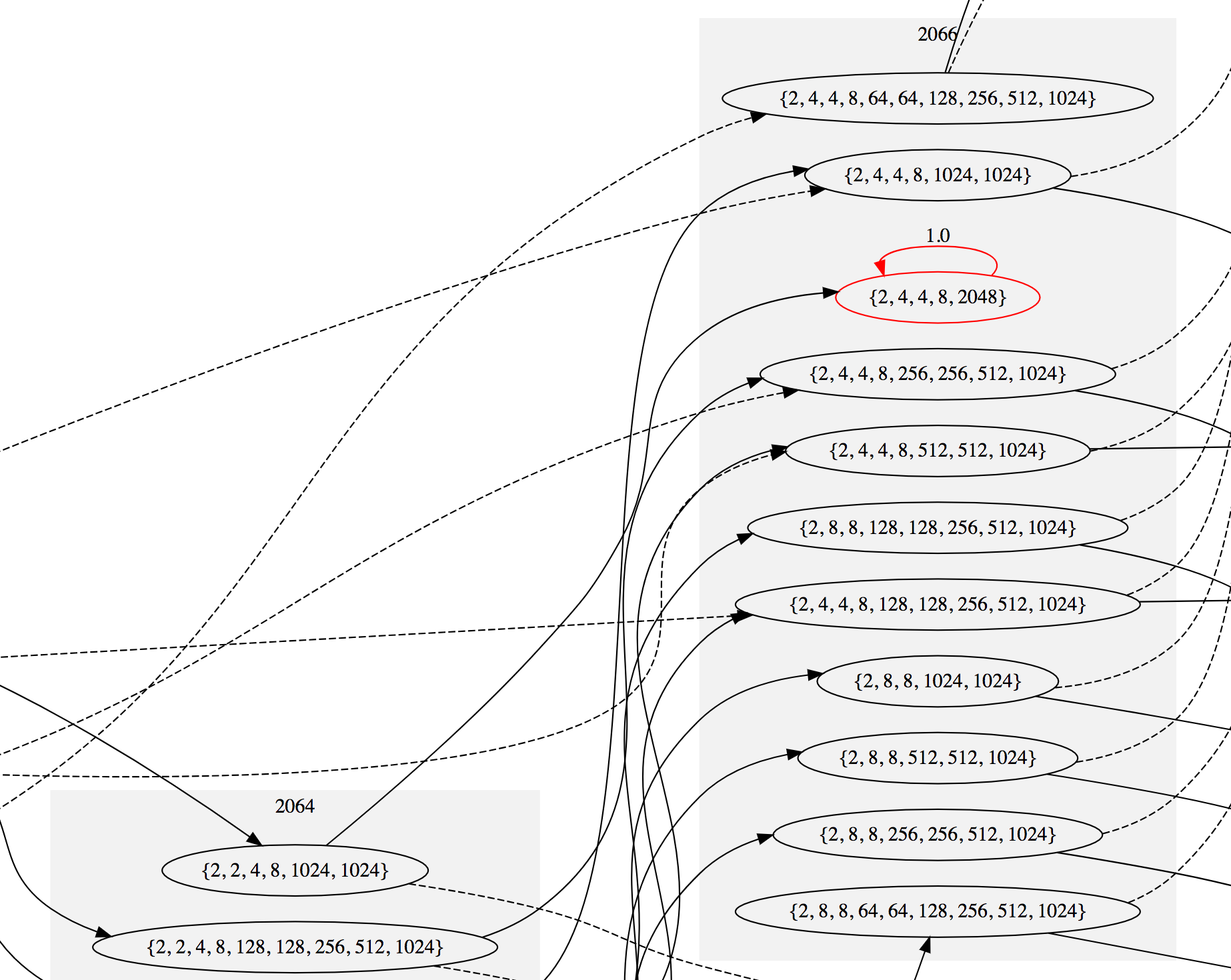
Screenshot of the end of the Markov chain

Если мы продолжим добавлять переходы до тех пор, пока не останется непоглощающих состояний, то в результате получим 3487 состояний, 26 из которых являются поглощающими; на этом завершится определение цепи Маркова. Схема полной цепи довольно велика, но если ваш компьютер способен справиться с 5-мегабайтным файлом SVG, то вот схема полной цепи (возможно, придётся немного прокрутить экран вниз, чтобы увидеть начало). Если уменьшить масштаб, то она будет выглядеть так:

Выборки из цепи

Теперь, когда мы вложили столько усилий в моделирование игры 2048 (в мешке) в виде цепи Маркова, нужно выяснить, сколько ходов потребуется для достижения всех поглощающих состояний. Простейшим способом для этого будет запуск симуляций. В каждой симуляции мы будем генерировать одну траекторию по цепи, начав с начального состояния, затем выбирая последующее состояние случайным образом, пропорционально переходным вероятностям, а затем повторяя процесс из этого состояния. После выполнения одного миллиона симуляций для количества ходов до победы выявляется следующее распределение:

Distribution of the number of moves to win, with the mean of 938.8 highlighted

Среднее, помеченное вертикальной синей линией, оказывается равным 938,8 ходам, исключая первый переход из начального состояния, со стандартным отклонением в 8,3 ходов. Итак, вот наш ответ на вопрос о минимальном ожидаемом количестве ходов до победы в игре!

Теория цепей Маркова также позволяет нам вычислить некоторые из этих свойств напрямую, с помощью хитрой математики. В Приложении А я покажу, как вычислить среднее число и стандартное отклонение для количества ходов, не используя симуляцию. Затем в Приложении Б я воспользуюсь некоторыми из свойств цепи, чтобы предложить хотя бы частичное объяснение формы кривой распределения.

Проверяем теорию практикой

Наконец, чтобы проверить эти результаты в реальной жизни, я много раз сыграл в 2048 (ради науки!) и в 28 выигранных играх я записал количество ходов, а также сумму тайлов на поле, когда я достиг тайла 2048 4:

Выписав эти числа в электронную таблицу и построив по ним график, я получил следующую диаграмму разброса:

Moves to Win and Tiles on Board for the 28 games I won

Я пометил синим минимальное ожидаемое количество ходов, плюс-минус одно стандартное отклонение, и красным сумму тайлов 2066, которая, как мы выяснили, является минимальной суммой тайлов, возможной при наличии тайла 2048.

Сумма тайлов на поле важна, потому что если она велика, то это обычно значит, что я совершил ошибку и загнал куда-то большой тайл, откуда не смогу объединить его с другим тайлом. Потом потребовалось гораздо больше ходов для повторного наращивания этого тайла на месте, откуда его можно объединить (или для изменения конфигурации поля для передвижения его в нужное место для объединения) с другим большим тайлом.

Если бы я хорошо играл в 2048, мы могли бы предсказать, что мои результаты сгруппируются в нижнем левом углу графика, и что большинство из них будут лежать между пунктирными синими линиями. На самом деле, как мы видим, хоть иногда я и подбираюсь к идеалу, результат не слишком стабилен — довольно много точек в верхнем правом углу с кучей лишних ходов и тайлов.

Этот график также подчёркивает тот факт, что наш анализ даёт нам только минимальное ожидаемое количество ходов. Было несколько игр, в которых мне везло и я выигрывал менее чем за 938,8 ходов, в том числе была победа с 927 ходами и суммой тайлов 2076. (Это второй слева результат в нижнем ряду подборки.) Так получилось потому, что в той игре мне случайно выпадало много тайлов 4, а ещё потому, что я не совершал серьёзных ошибок, требовавших лишних ходов.

В принципе, есть ненулевая вероятность того, что мы можем выиграть игру всего за 519 ходов. Мы можем определить это, пройдя по цепи, всегда выбирая переход в сторону 4 и считая количество переходов, необходимых для достижения тайла 2048. Однако вероятность такого исхода равна $0,1^{521}$ , или $10^{-521}$ . В наблюдаемой нами Вселенной всего примерно $10^{80}$ атомов, так что не стоит, затаив дыхание, ждать, что такая игра выпадет именно вам. Также, если нам очень не повезёт и мы всегда будем получать тайлы 2, мы всё равно сможем выиграть всего за 1032 ходов. Такая игра гораздо более вероятна, её вероятность равна $0,9^{1034}$ , что равно примерно равно $10^{-48}$ , так что, скорее всего, и такой игры не стоит ждать, затаив дыхание. Среднее в 938,8 ходов гораздо ближе к 1032, чем 519, потому что вероятность появления тайлов 2 гораздо выше, чем у тайлов 4.

Заключение

В этой части мы рассмотрели способ создания цепи Маркова, моделирующей эволюцию игры 2048 в случае, когда всегда возможно объединение одинаковых тайлов. Благодаря этому мы смогли применить техники теории поглощающих цепей Маркова для вычисления интересных свойств игры, и, в частности, выяснили, что в среднем для победы требуется не менее 938,8 ходов.

Основное упрощение, позволившее нам использовать этот подход, заключается в игнорировании структуры поля. То есть мы предположили, что бросаем тайлы в мешок, а не размещаем их на поле. Во второй части я планирую рассмотреть случай, когда мы учитываем структуру поля. Мы узнаем, что количество состояний, которое нужно рассмотреть, становится на много порядков больше (хотя, возможно, и не настолько больше, как можно подумать), и поймём, что нам придётся покинуть мир цепей Маркова, перейдя в мир марковских процессов принятия решений, что позволит нам вернуть в уравнения игрока. В принципе, мы сможем полностью «решить» игру, то есть, найти, возможно, оптимальный способ игры.

Приложение А: анализ цепи Маркова

После задания цепи Маркова, мы можем привлечь мощь математики для выполнения расчётов её свойств без симуляции. Многие из этих вычислений возможны только потому, что наша цепь Маркова принадлежит к особому виду цепей Маркова, называемому поглощающей цепью Маркова.

Чтобы относиться к поглощающим цепям, цепь Маркова должна соответствовать следующим критериям:

В ней должно быть хотя бы одно поглощающее состояние. Как мы видели выше, в нашей цепи существует 26 поглощающих состояний, по одному на каждое выигрышное состояние с тайлом 2048.
Любое состояние может достичь поглощающего состояния за конечное число переходов. Один из способов определить это — убедиться, что в цепи нет других циклов, кроме чем для поглощающих состояний: за исключением поглощающих состояний цепь является направленным ациклическим графом.

Переходная матрица

Теперь, когда мы определили, что имеем поглощающую цепь Маркова, следующим шагом будет написание её переходной матрицы в каноническом виде. Переходная матрица — это матрица, упорядочивающая переходные вероятности, которые для нашей цепи мы определили выше, такая, что элемент $(i, j)$ является вероятностью перехода из состояния $i$ в состояние $j$ .

Чтобы переходная матрица $\mathbf{P}$ поглощающей цепи с $r$ поглощающих состояний и $t$ невозвратных (то есть непоглощающих) состояний могла быть в каноническом виде, должна иметься возможность разбить её на четыре меньших матрицы $\mathbf{Q}$ , $\mathbf{R}$ , $\mathbf{0}$ и $\mathbf{I}$ , таких, что:

$\mathbf{P} = \left( \begin{array}{cc} \mathbf{Q} & \mathbf{R} \\\ \mathbf{0} & \mathbf{I}_r \end{array} \right)$

где $\mathbf{Q}$ — это матрица $t \times t$ , описывающая вероятность перехода из одного невозвратного состояния в другое невозвратное состояние, $\mathbf{R}$ — это матрица $t \times r$ , описывающая вероятность перехода из невозвратного состояния в поглощающее состояние, $\mathbf{0}$ обозначает матрицу $r \times t$ нулей, а $\mathbf{I}_r$ — это переходная матрица для поглощающих состояний, являющаяся единичной матрицей $r \times r$ .

Чтобы преобразовать переходную матрицу нашей цепи в канонический вид, нам нужно определиться с порядком состояний. Достаточно будет упорядочить состояния (1) по тому, являются ли они поглощающими (поглощающие состояния идут последними), затем (2) по сумме их тайлов (по возрастанию) и, наконец, (3) в лексическом порядке, чтобы избавиться от зависимостей. Если мы сделаем это, то получим следующую матрицу:

The full transition matrix for the absorbing Markov chain

Она довольно большая, а именно, размером $3487 \times 3487$ , поэтому при уменьшении масштаба выглядит почти диагональной, но если мы приблизим правый нижний угол, то увидим, что у неё есть структура, и, в частности, есть канонический вид, к которому мы стремимся:

The lower right hand corner of the transition matrix for the absorbing Markov chain, which shows more structure

Фундаментальная матрица

Получив канонический вид переходной матрицы, дальше мы используем её для нахождения того, что называется фундаментальной матрицей цепи. Она позволить нам вычислить ожидаемое количество переходов до поглощения, то есть мы (наконец-то!) найдём ответ на наш исходный вопрос.

Фундаментальная матрица $\mathbf{N}$ задаётся относительно $\mathbf{Q}$ тождественным равенством

$\mathbf{N} = \sum_{k=0}^{\infty} \mathbf{Q}^k\mathbf{N} = \sum_{k=0}^{\infty} \mathbf{Q}^k$

где $\mathbf{Q}^k$ обозначает $k$ -тую степень матрицы $\mathbf{Q}$ .

Элемент $(i, j)$ $\mathbf{N}$ имеет определённую интерпретацию: это ожидаемое число раз, которое мы войдём в состояние $j$ , если будем следовать по цепи, начиная с состояния $i$ . Чтобы увидеть это, мы можем заметить, что как элемент $(i, j)$ матрицы $\mathbf{Q}$ является вероятностью перехода из состояния $i$ в состояние $j$ за один переход, так и элемент матрицы $\mathbf{Q}^k$ является вероятностью входа в состояние $j$ ровно за $k$ переходов после входа в состояние $i$ . Если для заданной пары состояний $i$ и $j$ мы суммируем упомянутые вероятности для всех $k \geq 0$ , то сумма будет включать в себя каждый раз, когда мы имеет возможность войти в состояние $j$ после состояния $i$ , взвешенный по соответствующей вероятности, что и даёт нам нужное ожидание.

К счастью, фундаментальную матрицу можно вычислить напрямую, без неприятного бесконечного суммирования, как обратную матрицу $\mathbf{I}_t - \mathbf{Q}$ , где $\mathbf{I}_t$ — это единичная матрица $t \times t$ . То есть, $\mathbf{N} = (\mathbf{I}_t - \mathbf{Q})^{-1}$ . (Доказательство этого будет домашним заданием для читателя!)

Ожидаемое число ходов до победы

Получив фундаментальную матрицу, мы можем найти ожидаемое число переходов из любого состояния $i$ к поглощающему состоянию с помощью суммирования всех элементов в ряду $i$ — иными словами, количество переходов до попадания в поглощающее состояние равно общему числу переходов, которое нам пришлось совершить во всех невозвратных состояниях по пути.

Мы можем получить эти суммы рядов сразу для всех состояний, вычислив произведение матрицы на вектор $\mathbf{N} \mathbf{1}$ , где $\mathbf{1}$ обозначает вектор-столбец $t$ . Поскольку $\mathbf{N} = (\mathbf{I}_t - \mathbf{Q})^{-1}$ , мы можем сделать это, решив линейную систему уравнений

$(\mathbf{I}_t - \mathbf{Q})\mathbf{t} = \mathbf{1}$

для $\mathbf{t}$ . Элемент в $\mathbf{t}$ , соответствующий начальному состоянию (пустому множеству $\left \{ \right \}$ ), является числом переходов. В этом случае, получаемое число равно 939,8. Для завершения нам нужно только вычесть $1$ , потому что переход из начального состояния не считается ходом. Это даёт нам конечный ответ — 938,8 ходов.

Также мы можем получить дисперсию для минимального числа ходов как

$2(\mathbf{N} - \mathbf{I}_t) \mathbf{t} - \mathbf{t} \circ \mathbf{t}$

где $\circ$ обозначает (покомпонентное) произведение Адамара. Для начального состояния получаем дисперсию 69,5, что даёт нам стандартное отклонение в 8,3 шагов.

Приложение Б: форма кривой распределения

Примечательно, что нам удалось вычислить и среднее, и дисперсию распределения ходов до победы из цепи Маркова с помощью фундаментальной матрицы. Однако неплохо было бы узнать, почему распределение получилось такой формы. Предлагаемый здесь мной подход является только приблизительным., но он достаточно близко соответствует эмпирическим результатам из симуляции и даёт нам кое-какую полезную информацию.

Мы начнём с возврата к сделанному ранее наблюдению: сумма тайлов на поле увеличивается с каждым переходом на 2 или на 4 (кроме первого перехода из начального состояния). Как мы увидим ниже, если мы были бы заинтересованы в получении конкретной суммы на поле, а не получении тайла 2048, то было бы довольно просто вычислить нужное количество переходов с помощью биномиального распределения.

Итак, следующий вопрос будет заключаться в том, какую сумму мы хотим получить. Из приведённого выше анализа цепи Маркова мы определили, что существует 26 поглощающих (выигрышных) состояний. Мы также увидели, что они находятся на разных «слоях сумм», то есть нет одной суммы, к которой мы стремимся, их несколько. Нам нужно знать, какова вероятность для каждого состояния стать поглощённым. Она называется вероятностью поглощения. Затем мы можем суммировать вероятности поглощения для каждого из поглощающих состояний в отдельном слое сумм, чтобы найти вероятность выигрыша с конкретной получившейся суммой.

Вероятности поглощения

К счастью, вероятности поглощения тоже можно найти из фундаментальной матрицы. В частности, мы можем получить их, решив линейные уравнения

$(\mathbf{I}_t - \mathbf{Q}) \mathbf{B} = \mathbf{R}$

для матрицы $\mathbf{B}$ размером $t \times r$ , чей элемент $(i, j)$ — это вероятность поглощения в состоянии $j$ , начиная со состояния $i$ . Как и раньше, нас интересуют вероятности поглощения, при начале из начального состояния. Построив график вероятности поглощения, мы увидим, что существует 15 поглощающих состояний, вероятности которых достаточно велики для отображения на графике (не менее $10^{-3}$ ):

Absorbing probabilities for the Markov chain

В частности, большинство игр завершается или состоянием $\left \{ 2,2,8,8,2048 \right \}$ , сумма которого равна 2068, или состоянием $\left \{2,4,16,2048\right \}$ , сумма которого 2070. Суммируя все поглощающие состояния по сумме слоёв, мы получаем полные вероятности суммы слоя:

Total absorbing probabilities by sum of tiles

Биномиальные вероятности

Теперь, когда у нас есть суммы, на которые можно нацелиться, и мы знаем насколько часто мы нацеливаемся на каждую, следующим будет такой вопрос: сколько ходов нужно сделать, чтобы получить конкретную сумму? Как замечено выше, мы можем воспринимать этот вопрос применительно к биномиальному распределению, которое позволяет нам вычислить вероятность заданного количества «успехов» из заданного количества «попыток».

В этом случае под «попыткой» мы будем подразумевать ход, а под «успехом» — ход, в котором игра даёт нам тайл 4; как показано выше, это происходит с вероятностью 0,1. «Неудачей» здесь является ход, в котором игра даёт нам тайл 2, что происходит с вероятностью 0,9.

С учётом такой интерпретации успехов, для того, чтобы получить заданную сумму $S$ за $M$ ходов, нам потребуется $\frac{S}{2} - M$ успехов из $M$ ходов. Так получается, потому что каждый ход прибавляет к сумме как минимум $2$ , что в целом даёт $2M$ , а каждый успех добавляет к сумме дополнительные $2$ , внося в общем $2 \left(\frac{S}{2} - M\right) = S - 2M$ . Складывая эти значения, мы получим нужную сумму $S$ .

Тогда совместная вероятность получения суммы $S$ за количество ходов $M$ является биномиальной, и в частности

$\mathrm{Pr}(M=m, S=s) = B\left(\frac{s}{2} - m; m, 0.1\right)$

где $B(k; n, p)$ — это функция распределения масс для биномиального распределения, которая даёт нам вероятность получения ровно $k$ успехов за $n$ попыток, где вероятность успеха равна $p$ , т.е.

$B(k; n, p) = {n\choose k}p^k(1-p)^{n-k}$

где $n \choose k$ обозначает биномиальный коэффициент.

Теперь, когда мы знаем целевую сумму $S$ , к которой стремимся, мы можем вычислить условное распределение ходов с учётом того, что сумма, которая нас интересует — из совместного распределения. То есть мы можем найти $\mathrm{Pr}(M | S)$ как

$\mathrm{Pr}(M | S) = \frac{\mathrm{Pr}(M, S)}{\mathrm{Pr}(S)}$

где $\mathrm{Pr}(S)$ получается из совместного распределения суммированием $M$ для каждой возможной суммы $S$ . Стоит заметить, что $\mathrm{P}(S)$ меньше единицы для каждой возможной суммы, потому что всегда существует вероятность того, что игра «перескочит» сумму, выдав нам тайл 4.

Получив все эти условные распределения для каждой целевой суммы, мы можем сложить их, взвешенные по общей вероятности поглощения для целевой суммы, чтобы получить общую вероятность. Это даёт нам довольно точное совпадение с распределением из симуляции:

Simulated and binomial mixture model distributions for minimum moves to win

Здесь симулированное распределение показано серыми столбцами, а цветными областями показаны каждое из условных распределений. Каждое условное распределение отмасштабировано согласно общей вероятности поглощения для его суммы, а также смещено на несколько ходов, потому что бо́льшие суммы в среднем требуют больше ходов.

Одна из интерпретаций этого результата: при оптимальной игре количество ходов до выигрыша сильно зависит от того, насколько быстро игрок сможет получить сумму достаточно большую, чтобы содержать тайл 2048, что, в свою очередь зависит от числа тайлов 4, следующего биномиальному распределению.

Благодарю Хоуп Томас и Нейта Стемена за правку черновиков этой статьи.