[Перевод] Фильм «Скрытые фигуры»: задачи из фильма и современный подход к расчетам орбиты и возвращения на Землю

Перевод поста Джеффри Брайанта (Jeffrey Bryant), Пако Джейна (Paco Jain) и Майкл Тротта (Michael Trott) «Hidden Figures: Modern Approaches to Orbit and Reentry Calculations».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации
Содержание
— Размещение спутника в определенном месте
— Константы и первичная обработка
— Вычисления
— Построение графика
— Как рассчитываются орбиты сегодня
Моделирование возвращаемого спутника
Вышедший недавно в кинотеатрах фильм Скрытые фигуры получил хорошие отзывы. Действие разворачивается в важный период истории США; в нем затрагивается также ряд тем вроде гражданских прав и космической гонки. В центре повествования — история Кэтрин Джонсон и ее коллег (Дороти Воган и Мэри Джексон) из NASA в период развертывания программы Меркурий и ранних исследований пилотируемых космических полетов. Внимание также акцентируется на драматической борьбе за гражданские права афро-американских женщин в NASA, происходившей в то время. Компьютеры в то время едва появились, так что способность Джонсон и ее коллег решать сложные навигационные задачи орбитальной механики без использования компьютера обеспечили важную проверку ранних компьютерных результатов.
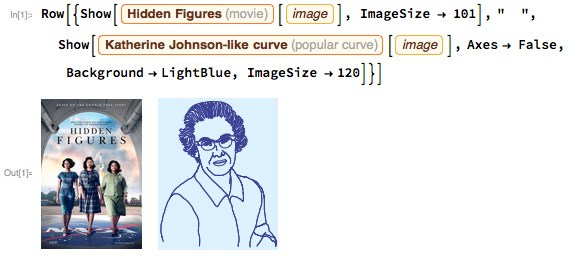
Я остановлюсь на двух аспектах ее научной работы, упомянутых в фильме: вычислениях орбиты и расчетах, связанных с вхождением в атмосферу. Для орбитальных вычислений я сначала сделал ровно то же, что и Джонсон, а затем применил более современный прямой подход с использованием инструментов Wolfram Language. В фильме упоминается о решении дифференциальных уравнений методом Эйлера; я же буду сравнивать этот метод с более современным и вычислю возвратную траекторию с помощью данных модели атмосферы, полученных непосредственно из Wolfram Language).
В фильме не освещаются детали решения математических задач командой Джонсон, однако того, что вы увидите, хватит, чтобы прочувствовать и сравнить подход, отображенный в фильме, с тем, который существует на данный момент.
Размещение спутника в определенном месте
Одна из самых ранних работ, в которой Джонсон была соавтором («Определение азимутального угла в точке выгорания для размещения спутника над выбранной точкой») имеет дело с проблемой проверки, может ли спутник быть размещен над определенной точкой Земли после определенного количества витков вокруг орбиты при определенной стартовой позиции (например, мыс Канаверал, штат Флорида) и траектории вращения. Подход, который команда Джонсон использовала для определения азимутального угла (угол, образованный вектором скорости космического аппарата в момент отключения двигателя, с фиксированным направлением, скажем, на север) для запуска ракеты основывался на других орбитальных параметрах. Это важный шаг для обеспечения правильного местонахождения астронавта для входа в атмосферу на Землю.

Константы и первичная обработка
В статье Джонсон определяет ряд констант и входных параметров, необходимых для решения задачи вручную. Отступлю немного, чтобы объяснить термин «выгорание», относящийся к остановке ракетного двигателя. После «выгорания» параметры орбиты как бы «замораживаются», и космический аппарат движется только под действием силы тяжести Земли (в соответствии с законами Ньютона). В этом разделе я следую тем определениям единиц, которые были приняты в статье.

Некоторые функции для удобства определены, чтобы взаимодействовать с углами в градусах вместо радиан. Это позволяет плавно регулировать время вычисления углов:
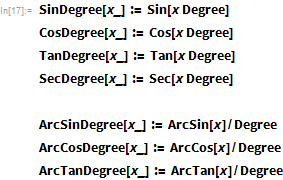
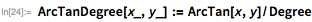
Джонсон описывает несколько других производных параметров, хотя интересно отметить, что иногда она принимает определенные значения для них, а не использует значения, полученные с помощью ее формул. Принятые ею значения часто были близки к значениям, полученным по формулам. Для простоты здесь используются значения из формул.
Semilatus rectum эллиптической орбиты:
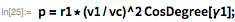
Угол в плоскости орбиты между перигеем и точкой выгорания:

Эксцентриситет орбиты:

Период орбиты:

Эксцентрическая аномалия:

Для описания следующего параметра проще будет процитировать оригинальную статью:»требование о том, чтобы спутник с точкой выгорания φ1, λ1 проходил через выбранную позицию φ2, λ2 после завершения n прохождений по орбите эквивалентно требованию, в соответствии с которым в ходе первого оборота спутник проходит через эквивалентное место с широтой φ2 так же, как и при выбранном положении, но с долготой λ2, смещенной в восточном направлении от λ2 на величину, достаточную для компенсации вращения Земли в течение n полных вращений, то есть полярного часового угла nωЕТ. Долгота этой эквивалентной позиции, таким образом, определяется соотношением»:

Время от перигея для угла θ:

Вычисления
Часть окончательного решения заключается в определении значения для промежуточных параметров δλ1–2е и θ2е. Это может быть сделано несколькими способами. Во-первых, я могу использовать ContourPlot для получения графического решения с помощью уравнений 19 и 20 из статьи:
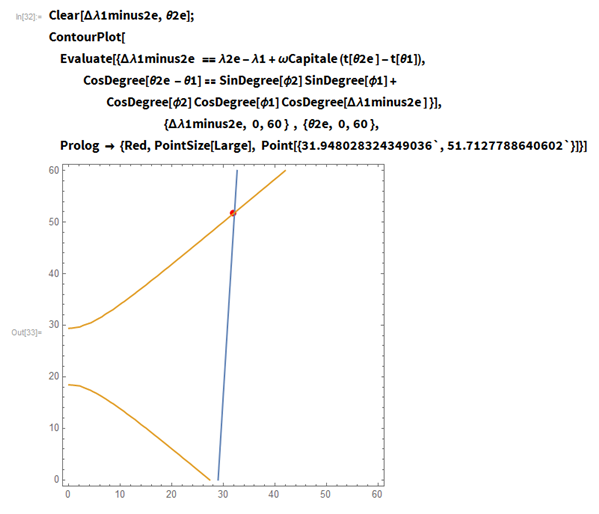
FindRoot можно использовать для нахождения численных решений:
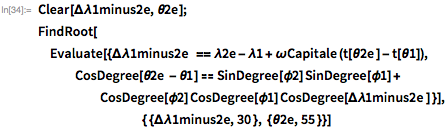
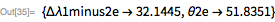
Конечно, у Джонсон не было доступа к функциям ContourPlot или FindRoot, так что в ее статье описывается итерационный метод. Я перевел методику, описанную в статье, на язык Wolfram, а также раскрыл ряд других параметров с помощью ее итерационного метода. Поскольку базовые выкладки рассчитаны для сферической формы Земли, поправки на сплющенности включены:

Графическое изображение значения θ2е для различных итераций демонстрирует быструю сходимость:


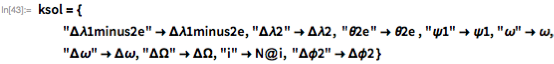
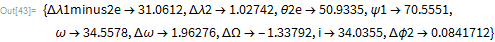
Я могу преобразовать метод в команде FindRoot следующим образом:

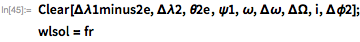
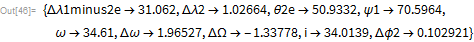
Интересно, что даже итерационные шаги поиска корня этой более сложной системы сходятся довольно быстро:


Построение графика
Когда орбитальные параметры определены, можно визуализировать решение. Во-первых, из предыдущих решений должны быть извлечены некоторые параметры:

Далее должны быть получены широта и долгота спутника в зависимости от азимутального угла:


φs и λs — широта и долгота как функция θs:


Наземный трек спутника может быть построен путем создания таблицы точек:

В статье Джонсон представлена схема орбитального решения, включая маркеры, отмечающие выгорание, а также выбранные и эквивалентные положения. Подобную схему легко воспроизвести:


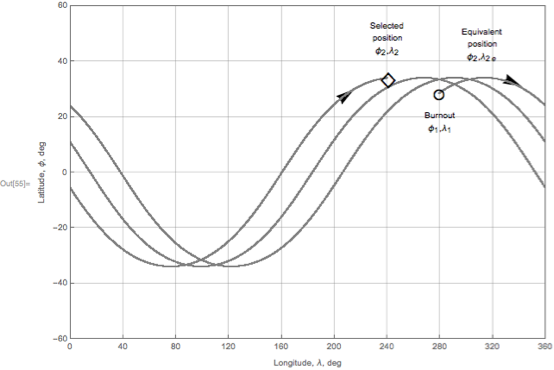
Вот ее оригинальная схема для сравнения:
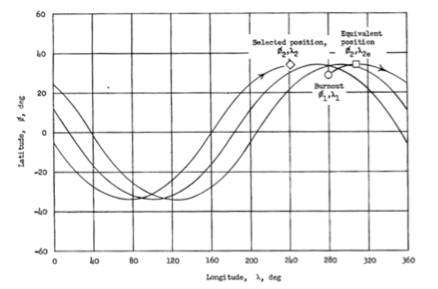
Более визуально полезная версия может быть построена с помощью функции GeoGraphics, которая преобразует геоцентрические координаты в геодезические:



Как рассчитываются орбиты сегодня
Сегодня практически у каждого из нас есть доступ к вычислительным ресурсам гораздо более мощным, чем те, что были у НАСА в 1960-е годы. Сейчас, используя только настольный компьютер и Wolfram Language, вы можете легко найти прямые численные решения задач орбитальной механики вроде тех, которыми занимались Кэтрин Джонсон и ее команда.
Чтобы вычислить азимутальный угол ψ с помощью более современных методов, давайте установим параметры для простой круговой орбиты, берущей свое начало после выгорания над Флоридой; предположим также, что Земля сферически симметрична (я не буду пытаться искать точное соответствие с данными из статьи Джонсон и переопределю некоторые величины, используя современную систему единиц СИ). Начиная с той же высоты околоземной орбиты, используемой Джонсон, и с помощью сферической тригонометрии несложно вывести начальные условия для нашей орбиты:


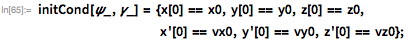
Соответствующие физические параметры могут быть получены непосредственно с помощью Wolfram Language:
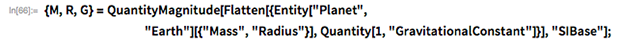
Далее я получил дифференциальное уравнение движения нашего космического корабля с учетом гравитационного поля Земли. Есть несколько способов моделирования гравитационного потенциала вблизи Земли. Предположим, что планета сферически симметрична и используем декартову систему координат:
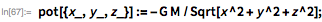
Кроме того, вы можете использовать более реалистичную модель гравитации Земли, где в качестве формы планеты берется сплюснутый эллипсоид вращения. Точная форма потенциала такого эллипсоида (при условии постоянной плотности массы эллипсоидальных оболочек) доступна с помощью EntityValue:

Для общего однородного трехосного эллипсоида потенциал содержит кусочные функции:


Здесь κ является наибольшим корнем выражения х2/(a2 + κ) + у2/(b2 + k) + z2/(c2 + κ) = 1. В случае, если мы имеем дело со сплющенным эллипсоидом, предыдущая формула может быть упрощена до элементарных функций…
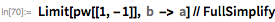
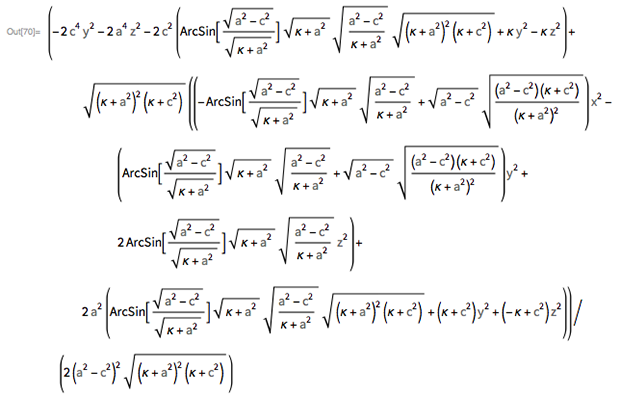
… где κ=((2 z2 (a2-c2+x2+y2)+(-a2+c2+x2+y2)2+z4)½-a2-c2+x2+y2+z2)/2.
Более простая форма, которую я буду использовать здесь, задается так называемой общепринятой формулой ускорения силы тяжести (IGF). В данной формуле учитываются отличия от сферически симметричного потенциала до второго порядка в сферических гармониках, и даются численно неотличимые от точного потенциала, на который ссылались ранее, результаты. В терминах четырех измеренных геодезических параметров потенциал IGF может быть определен следующим образом:

Я мог бы легко использовать даже еще более точные значения для силы тяжести с помощью функции GeogravityModelData. В исходном положении потенциал IGF только на 0,06% отклоняется от приближения высокого порядка:

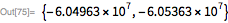
С этими функциональными формами потенциала нахождение орбитального пути требует вычисления градиента потенциала, чтобы получить вектор гравитационного поля, с применением затем третьего закона Ньютона. Я получаю орбитальные уравнения движения для двух моделей гравитации:
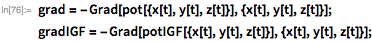

Теперь я готов использовать силу NDSolve для вычисления орбитальных траекторий. Однако перед тем, как сделать это, будет неплохо отобразить орбитальный путь в виде кривой в трехмерном пространстве. Чтобы встроить эти кривые в контекст, я построил их по текстурной карте поверхности Земли и спроецировал на сферу. Здесь я построил нужные графические объекты:




В то время, как орбитальный путь, вычисляемый в инерциальной системе отсчета, образует периодическую замкнутую кривую, получается, что космический корабль будет проходить через различные точки на поверхности Земли во время каждого последующего оборота. Я могу визуализировать этот эффект, добавив дополнительное время вращения к решениям, которые я получаю от функции NDSolve. Примем, что число орбитальных периодов будет три (по аналогии с полетом Джона Гленна), я использовал функцию Manipulate чтобы увидеть, как орбитальный путь зависит от азимутального угла ψ, подобно исследованию в статье Джонсон. Я построю один график для сферической Земли (белый цвет) и другой, зеленый, чтобы продемонстрировать эффект сплюснутости (обратите внимание, что расхождение увеличивается с каждым витком):

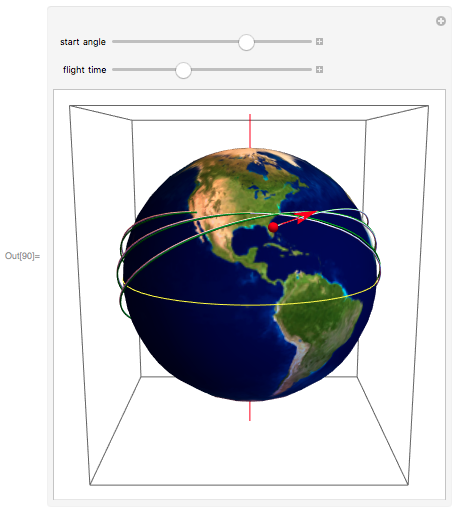
В документе, который прилагается к этой записи, вы сможете увидеть функцию Manipulate в действии; обратите внимание на скорость, с которой находится каждое новое решение. Хочется надеяться, что Кэтрин Джонсон и ее коллеги в НАСА были бы впечатлены!
Теперь, изменяя угол ψ в точке выгорания, легко вычислить положение космического аппарата после, скажем, трех оборотов:



В фильме также в связи с фазой возвращения упоминается метод Эйлера. После решения исходной задачи нахождения азимутального угла, как это было сделано в предыдущих разделах, пришло время вернуться на Землю. Для замедления вращения происходит запуск ракет, и затем, при переходе из безвоздушной среды космоса в атмосферу, происходит сложный комплекс событий. Для благополучного возвращения космонавта на Землю долны быть приняты во внимание такие факторы, как изменение плотности атмосферы, быстрое торможение и фрикционный нагрев. Необходимо решить проблемы высоты, скорости и ускорения как функции времени. Этот набор проблем может быть решен с помощью метода Эйлера, как это было сделано Кэтрин Джонсон, или с помощью функциональных возможностей решения дифференциальных уравнений в Wolfram Language.
Для простых дифференциальных уравнений можно получить подробное пошаговое решение с помощью указанного метода квадратур. Эквивалентом известной формулы Ньютона F = mа для зависящей от времени массы m(t) является так называемое уравнение для идеальной ракеты (в одном измерении)…
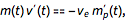
… где m(t) — масса ракеты, vе скорость выхлопа ракетного двигателя, и m’p(t) — производная массы топлива от времени. При постоянной m’p(t) структура уравнения оказывается относительно простой и легко разрешимой в замкнутой форме:

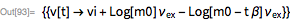
Имея начальные и конечные условия для массы, я получаю знаменитое уравнение движения ракеты (К.Э. Циолковский, 1903):



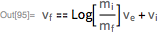



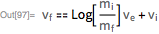
Детали решения этого уравнения с конкретными значениями параметров я могу взять из Wolfram|Alpha. Вот эти детали вместе со сравнением с точным решением, а также с другими методами численного интегрирования:


Следуя сюжету фильма, я реализую теперь минималистическую модель процесса повторного входа. Начнем с определения параметров, которые имитируют полет Гленна:

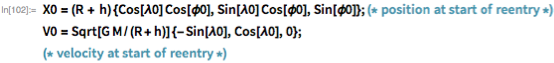
Я полагаю, что в процессе торможения используется 1% от тяги двигателя первой ступени, и длится он, скажем, 60 секунд. Уравнение движения:

Здесь Fgrav — сила тяжести, Fexhaust (t) — зависящая от времени сила двигателя, и сила трения Ffriction (x(t), v(t)). Последняя зависит как от плотности воздуха в положении x(t), так и от закона трения для v(t).
Для плотности воздуха, которая зависит от высоты, я могу использовать функцию StandardAtmosphereData. Я учитываю ее также из-за парашюта, который открывается на высоте около 8,5 км над землей:

Это дает следующий набор связанных нелинейных дифференциальных уравнений, которые необходимо решить. Функция WhenEvent[…] указывает на конец построения решения ДУ, когда капсула достигает поверхности Земли. Я использую векторные значения положения и скорости переменных X и V:

С учетом этих определений для веса, выхлопных газов и силы трения воздуха точки зрения…
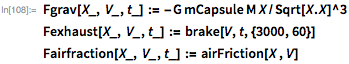
… результирующая сила может быть найдена с помощью:
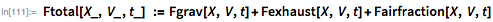
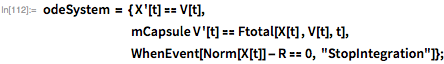
В этой модели я пренебрег вращением Земли, внутренними углами вращения капсулы, активными изменениями угла полета, сверхзвуковыми эффектами силы трения и многим другим. Уравнения, решаемые Кэтрин Джонсон:


Эту систему уравнений просто решить численно, если дополнить ее начальным положением и скоростью. Для этого нужно всего лишь обратиться к функции NDSolve. Мне не придется беспокоиться об используемом методе, управлении размером шага, контроле ошибок и так далее, потому что Wolfram Language автоматически выбирает те значения, которые гарантируют значимые результаты:
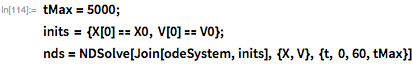

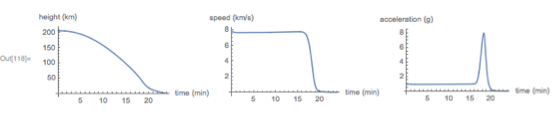
Здесь представлен график высоты, скорости и ускорения в зависимости от времени:


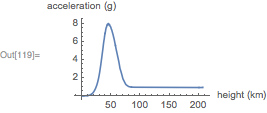
Кривая зависимости от высоты вместо времени демонстрирует, что экспоненциальное возрастание плотности воздуха отвечает за сильное торможение. Это не связано с парашютированием, которое происходит на относительно малой высоте. Пик замедления происходит на очень большой высоте, когда капсула быстро переходит из вакуума к атмосферной среде:

А вот график вертикальной и тангенциальной скоростей капсулы в процессе повторного входа:

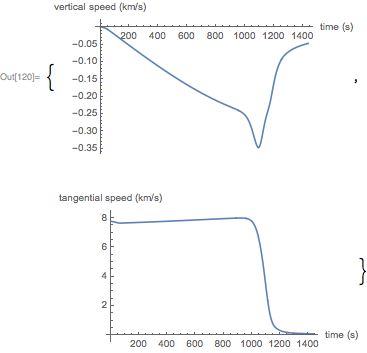
Теперь я повторю численное решение методом Эйлера с фиксированным шагом:


Качественно это решение выглядит так же, как и предыдущее:
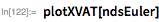

Для используемого размера шага интегрирования по времени накопленная ошибка составляет порядка нескольких процентов. Меньшие размеры шага будут уменьшать ошибку:
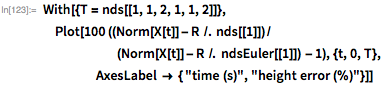

Обратите внимание, что время посадки, предсказываемое методом Эйлера, отклоняется всего на 0,11% по сравнению с предыдущим временем (для сравнения: если бы я решал уравнение двумя современными методами, — скажем, «BDF» или «Adams», то ошибка была бы меньше на несколько порядков).
В процессе повторного входа генерируется большое количество тепла. Здесь нужен теплозащитный экран. На какой высоте производится наибольшее количество тепла на единицу площади Q? Не вдаваясь в подробности, я могу, чисто из соображений размерности, применить гипотезу  :
:




Много чего интересного можно было бы вычислить (Hicks 2009), но точно так же, как фильм должен был закончиться, так и я теперь должен завершить мою статью. Надеюсь, вы простите меня за мои слова: с Wolfram Language вы можете сделать все, что захотите.
Комментарии (1)
18 апреля 2017 в 14:20
0↑
↓
Вот это я понимаю статья для Хабра!
Большое спасибо вам за ваш труд!
