[Из песочницы] Задача о конфетах (улучшаем результат)
28 сентября viktorpanasiuk опубликовал задачу, решение которой призвано снизить издержки производства небезизвестной кондитерской фабрики, сделав её товар более конкурентноспособным на рынке и более доступным покупателю.
Необходимо было найти максимально допустимое отклонение массы конфеты при ее производстве, чтобы нетто коробки, состоящей из 12 штук их, не выходило за пределы 310±7 грамм в 90% случаев. Закон распределения считать нормальным.
Был получен ответ, что если среднеквадратичное отклонение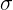 
массы конфеты при производстве не превышает 
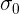=1,2248, то данная величина не ограничена сверху.
Под катом вас ожидает улучшение полученного результата по модулю некоторых, как мне кажется — разумных, предположений. Дальнейшее изложено недостаточно строго, но всё же требует знаний математического анализа и теории вероятности в объёме технического вуза.
Пусть масса коробки — нормально распределенная случайная величина. Пусть массы конфет это одинаковые независимые в совокупности абсолютно непрерывные случайные величины, с математическим ожиданием 310/12. Пусть при этом плотность распределения является симметричной относительно математического ожидания и не возрастает правее математического ожидания (соответственно не убывает левее). Пусть среднеквадратичное отклонение масс конфет 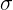и 
.
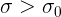Оценим снизу максимально допустимое отклонение массы конфеты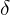 
.
Так как математическое ожидание масс конфет на решение не влияет, в дальнейшем я буду оперировать центрированными случайными величинами.
Очевидно, при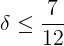 
требуемуе условие будет выполнено с вероятностью 1. Ниже я покажу как данная оценка может быть улучшена до 
.
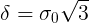Пусть f — плотность распределения массы конфеты. Тогда в силу определения условной вероятности новая плотность распределения будет иметь вид: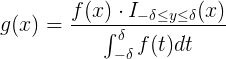 
.
При этом новая случайная величина должна иметь среднеквадратичное отклонение .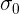
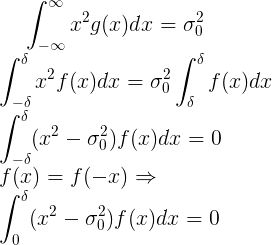
Разрешив полученное уравнение относительно 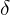получаем нужную нам оценку при известной плотности распределения f.
Для дальнейшего рассуждения понадобится лемма:
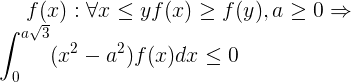
Доказательство:
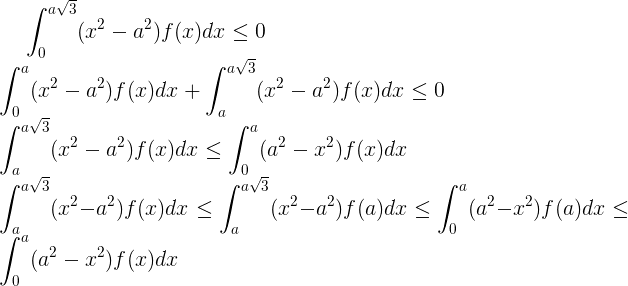
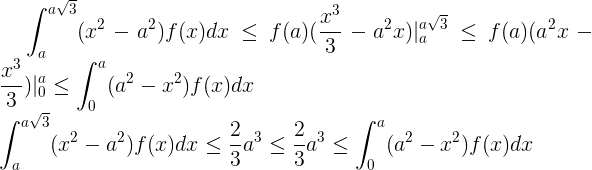
чтд.
Заметим, что если при x<a есть множество положительной меры где f(x)>f(a) или при a <x < a 3^(1/2) есть множество положительной меры где f(x) < f (a) то неравенство в формулировке леммы будет строгим.
Легко показать, что если f — плотность распределения равномерной случайной величины с математическим ожиданием 0 и 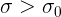, то .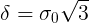
Тогда, применив лемму, получаем что если распределение массы конфет неизвестно, но принадлежит описанному классу то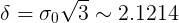 
.
Что ещё можно сделать: оценить применимость ЦПТ (через критерий хи квадрат или неравенство Берри — Эссеена), найти на сколько полученная оценка хуже оптимальной при известных распределениях.
Спасибо тем кто дочитал до конца. Любите математику.
